Teoria dos conjuntos: A base da matemática com exemplos e demonstrações.

Introdução

Você já parou para pensar no que é, de fato, um conjunto?
Desde cedo, lidamos com coleções de objetos: o conjunto dos seus livros preferidos, das cores que você gosta ou dos números pares menores que 10.
A Teoria dos Conjuntos é a base da matemática moderna e, neste artigo, vamos explorar de forma simples — mas com rigor técnico — os conceitos fundamentais e algumas demonstrações práticas.

O que é um Conjunto?

Um conjunto é uma coleção bem definida de objetos, chamados de elementos.
Esses elementos podem ser números, letras, pessoas ou qualquer outra coisa.

Exemplo:
O conjunto dos números naturais menores que 5 é:

$$A = \{0, 1, 2, 3, 4\}$$

Notação comum: usamos letras maiúsculas para representar conjuntos e chaves {} para listar os elementos.

Relações de Pertinência e Inclusão

• Pertinência: diz respeito a um elemento pertencer ou não a um conjunto.

  Notação:

  $$2 \in A \quad \text{(o número 2 pertence ao conjunto A)}$$ $$5 \notin A \quad \text{(o número 5 não pertence ao conjunto A)}$$

• Inclusão: trata-se de um conjunto estar contido em outro.

  Se $B = \{1, 2\}$, então:

  $$B\subset A\text{(B }\acute{\text{e}}\text{ subconjunto de A)}$$

Operações entre Conjuntos

União ( $A \cup B$ )

A união de dois conjuntos é o conjunto formado por todos os elementos que pertencem a A, a B ou a ambos.

Exemplo:

$$A = \{1, 2, 3\}, \quad B = \{3, 4, 5\}$$ $$A \cup B = \{1, 2, 3, 4, 5\}$$

Interseção ( $A \cap B$ )

A interseção de dois conjuntos é formada apenas pelos elementos que estão em ambos.

Exemplo:

$$A \cap B = \{3\}$$

Diferença ( $A - B$ )

A diferença entre dois conjuntos A e B é o conjunto dos elementos que estão em A mas não estão em B.

Exemplo:

$$A - B = \{1, 2\}$$

Diagramas de Venn

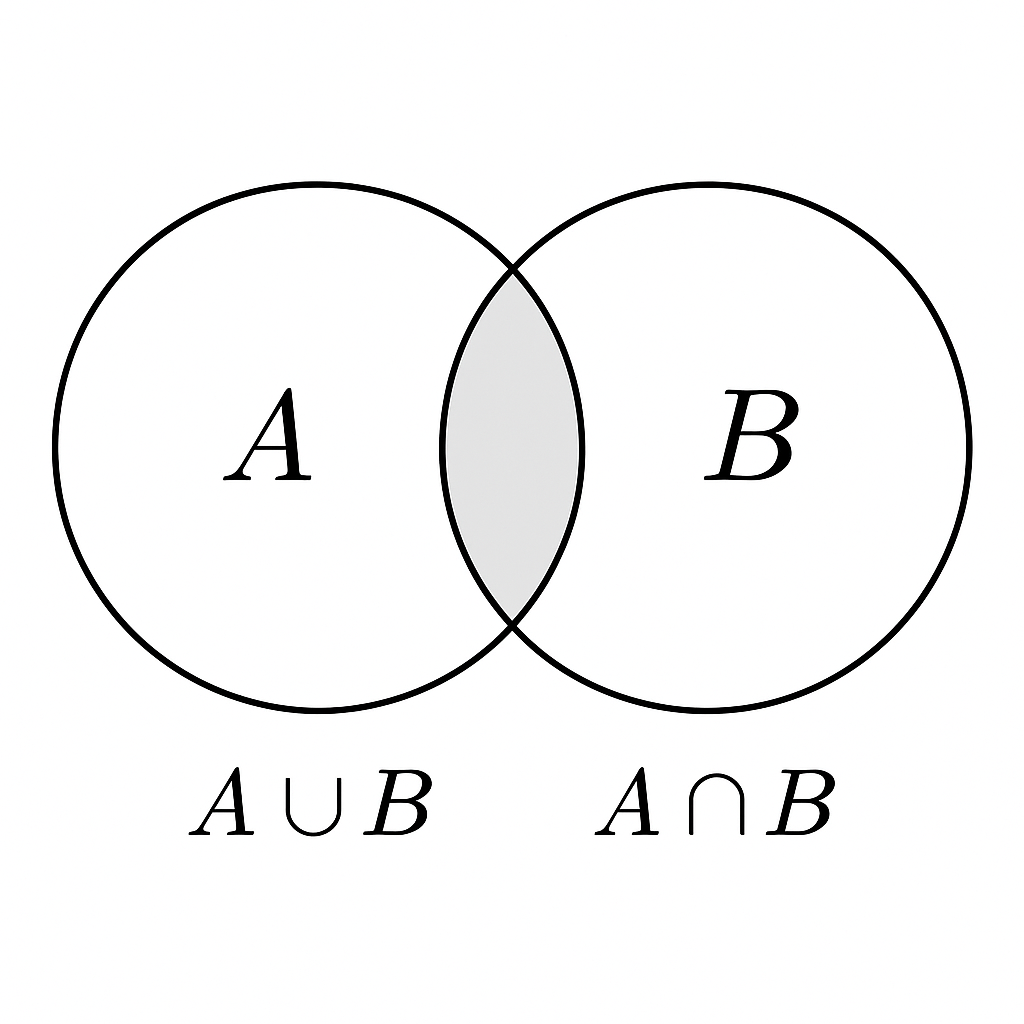
Os diagramas de Venn ajudam a visualizar relações entre conjuntos.

Representação:

• Duas circunferências sobrepostas;

• A parte comum representa $A \cap B$ (interseção);

• A área total representa $A \cup B$ (união).

Conjunto das Partes (𝒫(A))

O Conjunto das Partes de um conjunto $A$ é o conjunto formado por todos os subconjuntos possíveis de $A$, incluindo o conjunto vazio $\emptyset$.

Exemplo:

Se:

$$A = \{1, 2\}$$

Então:

$$\mathcal{P}(A) = \{\emptyset, \{1\}, \{2\}, \{1,2\}\}$$

Fórmula geral:
Se $A$ tem $n$ elementos, então $\mathcal{P}(A)$ tem $2^n$ subconjuntos.

Produto Cartesiano

O Produto Cartesiano de dois conjuntos $A$ e $B$ é o conjunto de todos os pares ordenados $(a, b)$, onde $a \in A$ e $b \in B$.

Exemplo:

Se:

$$A = \{1, 2\}, \quad B = \{a, b\}$$

Então:

$$A \times B = \{(1,a), (1,b), (2,a), (2,b)\}$$

O produto cartesiano é fundamental para entender relações, funções e a construção do plano cartesiano.

Demonstração Técnica: Propriedade da União

Propriedade:
Se $A \subset B$, então $A \cup B = B$.

Demonstração:

Sabemos que:

• Se $A \subset B$, então todo elemento de $A$ também pertence a $B$.

Então:

• $A \cup B$ reúne todos os elementos de $A$ e de $B$;

• Mas como todos de $A$ já estão em $B$, a união não adiciona nada novo.

Portanto:

$$A \cup B = B$$

✔️ Demonstrado!

Probleminha Prático

Desafio:
Dado o conjunto $A = \{1,2,3\}$ e o conjunto $B = \{2,3,4\}$:

1. Encontre $A \cup B$ (união).

2. Encontre $A \cap B$ (interseção).

3. Liste $\mathcal{P}(A)$ (conjunto das partes de A).

4. Calcule $A \times B$ (produto cartesiano).

Respostas:

1. $A \cup B = \{1,2,3,4\}$

2. $A \cap B = \{2,3\}$

3. $\mathcal{P}(A) = \{\emptyset, \{1\}, \{2\}, \{3\}, \{1,2\}, \{1,3\}, \{2,3\}, \{1,2,3\}\}$

4. $A \times B = \{(1,2), (1,3), (1,4), (2,2), (2,3), (2,4), (3,2), (3,3), (3,4)\}$

Conclusão

A teoria dos conjuntos é a linguagem que descreve toda a matemática.
Ao entender conjuntos, operações e suas propriedades, você cria uma base sólida para avançar para temas mais complexos — de álgebra a análise de dados.

E o melhor: tudo começa com uma simples coleção de objetos!

FIM