Campo de força gravitacional repulsivo.

 Uma Força Gravitacional Repulsiva?

Neste trabalho, apresento uma proposta ousada e fascinante: a criação de um campo de força capaz de repelir a gravidade. Isso mesmo — em vez de atrair, como estamos acostumados a pensar, esse campo teria o poder de empurrar para longe qualquer partícula material que se aproxime, funcionando quase como um "escudo invisível".

Além de repelir, esse campo também teria a incrível capacidade de anular o momento — ou seja, o impulso — das partículas que tentam atravessá-lo, inclusive a luz e o calor na faixa do infravermelho. Com isso, esse escudo se tornaria um isolante térmico perfeito. Imagine uma nave espacial envolvida por esse campo: nenhuma temperatura externa conseguiria afetá-la. Em teoria, ela poderia até entrar e sair do Sol sem sofrer danos ou colocar em risco a vida de quem está a bordo.

Esse mesmo campo também teria outra vantagem surpreendente: ao reduzir drasticamente o atrito com a atmosfera, uma aeronave equipada com ele poderia atingir velocidades altíssimas sem superaquecer, abrindo caminho para uma nova era de transporte aéreo e espacial.

A base para tudo isso? Um processo de reversão e intensificação da gravidade, feito por meios eletromagnéticos. Em outras palavras, estamos falando de uma nova forma de "brincar com a gravidade", usando a própria natureza contra ela mesma.

Massa, Matéria Escura e o Campo de Higgs

As equações do campo de Higgs, que são a base para entendermos como as partículas adquirem massa, nos dão pistas importantes sobre a natureza da gravidade e suas possíveis "faces". Partindo da ideia de que a massa gerada pelo campo de Higgs é também a massa gravitacional, podemos explorar uma hipótese curiosa: e se essa massa surgir do equilíbrio entre dois tipos opostos — uma massa gravitacional positiva e outra negativa?

Nesse contexto, propõe-se que a massa gravitacional negativa não é algo imaginário ou fictício. Ela pode ser real, concreta, e está presente no universo como aquilo que chamamos de matéria escura. Já a massa positiva seria aquilo que chamamos de partícula, aquilo que compõe tudo o que conseguimos ver, tocar e medir.

A equação que rege essa dinâmica pode ser expressa matematicamente como:

$$\nabla_{\mu} \nabla^{\mu} \varphi_a + \frac{1}{2} \left( m_0^2 - f^2 \varphi_b \varphi_b \right) \varphi_a = 0$$

Esse formalismo descreve a evolução do campo escalar $\varphi_a$, que representa o comportamento da massa em função da interação com o próprio campo de Higgs. O termo $m_0^2$ está relacionado à massa original do campo, enquanto o fator de correção $f^2 \varphi_b \varphi_b$ representa uma interação interna entre os componentes do campo — uma espécie de “autoajuste” dinâmico.

Quando esse equilíbrio interno muda, a massa aparente do sistema pode oscilar entre positiva e negativa. É aí que entra a nossa interpretação: a massa positiva dá origem às partículas que compõem a matéria visível, enquanto a massa negativa se manifesta como uma força gravitacional repulsiva — aquilo que chamamos de matéria escura.

Ao “quebrar” o campo de Higgs em seus componentes, surge essa dualidade: de um lado, a massa visível que chamamos de matéria; do outro, a parte invisível, repulsiva, que chamamos de matéria escura. Nesse processo, o bóson de Goldstone representa uma simetria oculta — uma espécie de elo entre esses dois mundos — enquanto o chamado mecanismo de Higgs marca a quebra espontânea dessa simetria, o momento em que o equilíbrio se desfaz e a massa aparece.

O fato do bóson de Higgs ter sido detectado em laboratório reforça essa visão: se ele realmente existe, então também existem os dois lados da massa — a positiva e a negativa. E com isso, a matéria escura deixa de ser apenas um mistério cósmico e passa a ser uma peça do mesmo quebra-cabeça.

A Possibilidade de Uma Gravidade Repulsiva

Tradicionalmente, tanto na teoria de Newton quanto na Teoria da Relatividade Geral de Einstein, a gravidade é tratada como uma força exclusivamente atrativa. Ela puxa, aproxima, une. E é com essa ideia que crescemos — de que a gravidade é o que nos mantém presos ao solo, o que guia os planetas em suas órbitas e estrutura o universo como conhecemos.

Mas a ciência, como a própria natureza, está sempre se reinventando.

Com o avanço dos estudos sobre a quantização da gravidade — ou seja, a tentativa de descrever a gravidade em termos das regras da mecânica quântica — surge uma possibilidade fascinante: a existência de forças gravitacionais repulsivas. Isso significa que, em certas condições, a gravidade pode não apenas atrair, mas também rejeitar — empurrar partículas para longe, como se criasse um escudo invisível.

É nesse ponto que nossa proposta ganha força.

Com base nessa visão moderna da gravidade, propomos um método para gerar um campo gravitacional repulsivo. Um campo que não apenas repele partículas materiais, mas também é capaz de desviar ou anular fótons — inclusive aqueles na faixa do infravermelho, responsáveis pela transmissão de calor. Isso abre caminho para aplicações surpreendentes: imagine uma nave espacial envolta por esse campo, capaz de atravessar ambientes extremos, como a atmosfera solar, sem sofrer superaquecimento ou danos estruturais.

Estamos falando, essencialmente, da criação de uma nova interação gravitacional — uma gravidade que, em vez de prender, liberta. E é com base em modelos matemáticos consistentes, reforçados por conceitos da física de partículas e da gravitação quântica, que avançamos para mostrar como isso é possível.

A Teoria por Trás do Campo Gravitacional Repulsivo

Em trabalhos anteriores, foi demonstrado que uma partícula pode sofrer variações em seu peso dependendo do lado de uma lâmina gravitacional em que ela se encontra. Suponhamos que, de um lado da lâmina, o peso da partícula seja dado por:

$$P = m_g g$$

onde $m_g$ é a massa gravitacional da partícula e $g$ é o campo gravitacional (com direção perpendicular à lâmina). Do outro lado da lâmina, esse peso se transforma em:

$$P' = m_g g' = \chi m_g g$$

Nessa equação, $\chi$ representa um fator de transformação gravitacional associado à lâmina. Ele depende das características da própria lâmina, mais precisamente da razão entre sua massa gravitacional ($m_g^0$) e sua massa inercial ($m_i^0$):

$$\chi = \frac{m_g^0}{m_i^0}$$

Quando $\chi = 1$, o peso da partícula permanece o mesmo nos dois lados. Mas quando $\chi \neq 1$, temos o chamado efeito de blindagem gravitacional (Gravitational Shielding), no qual a lâmina modifica a intensidade do campo gravitacional sentido por qualquer objeto que a atravesse.

Superposição de Blindagens

Agora imagine que temos duas blindagens gravitacionais paralelas, com fatores $\chi_1$ e $\chi_2$. A partícula, ao atravessá-las, sofre uma transformação em sua massa gravitacional equivalente:

$$m_g' = \chi_1 \chi_2 m_g$$

Esse raciocínio pode ser generalizado. Se tivermos n blindagens gravitacionais sucessivas, com fatores $\chi_1, \chi_2, \chi_3, \ldots, \chi_n$, o efeito acumulado será equivalente a uma única blindagem com fator:

$$\chi_{\text{total}} = \chi_1 \cdot \chi_2 \cdot \chi_3 \cdots \chi_n$$

Logo, tanto a massa gravitacional efetiva da partícula quanto o campo gravitacional resultante serão multiplicados por esse fator total:

$$m_g^{(n)} = \chi_{\text{total}} \cdot m_g \quad \text{e} \quad g^{(n)} = \chi_{\text{total}} \cdot g$$

Essa multiplicação sucessiva permite, teoricamente, reduzir — ou até inverter — o efeito gravitacional. E, quando o valor de $\chi_{\text{total}}$ se torna negativo ou suficientemente pequeno, entra em cena o tão sonhado campo gravitacional repulsivo.

Modelo Conceitual – Camadas de Blindagem Gravitacional

Imagine um feixe de linhas verticais representando a direção e intensidade do campo gravitacional tradicional (atrativo). Cada camada de blindagem atua como um filtro, alterando o "peso" do campo:

Ilustração - Campo Gravitacional com Blindagens Sucessivas

Legenda:

• Linhas verticais azuis → Campo gravitacional original (sentido atrativo).

• Camadas cinzas → Lâminas com fatores $\chi_i$.

• Linhas vermelhas → Campo resultante (podendo ser mais fraco, nulo ou até invertido).

 Blindagens Gravitacionais Planas e Esféricas

Quando usamos uma blindagem gravitacional esférica — como se fosse uma casca ou escudo que envolve um volume — e o seu raio $b$ é muito pequeno, acontece um efeito interessante:

Qualquer partícula posicionada dentro dessa casca esférica vai apresentar uma massa gravitacional modificada. Em vez de sentir o peso normal devido ao campo gravitacional externo, ela passa a ter sua massa gravitacional alterada por um fator $\chi$, ou seja:

$$m'_g = \chi \cdot m_g$$

Onde:

• $m_g$ é a massa gravitacional da partícula fora da casca;

• $m'_g$ é a massa gravitacional que ela "sente" dentro da blindagem;

• $\chi$ é o fator de blindagem gravitacional gerado pela estrutura.

Esse fator $\chi$, como já vimos, depende das propriedades da blindagem (materiais, energia envolvida, campo aplicado etc.). O efeito geral é como se o campo gravitacional fosse suavizado, anulado ou até invertido dentro dessa casca, dependendo de quanto $\chi$ se afasta da unidade.

Efeito de Blindagem Gravitacional (BG)

Quando temos um sistema com blindagem gravitacional (BG) — por exemplo, uma lâmina que gera esse efeito — a gravidade é modificada de um lado para o outro.

Se do lado A da blindagem a gravidade tem intensidade $g_r$ (considerando que a direção é perpendicular à lâmina), então, do lado B, a gravidade passa a ser:

$$g_r' = \chi \cdot g_r$$

Ou seja, o campo gravitacional "do outro lado" é proporcional ao original, mas modulado pelo fator $\chi$, que caracteriza o quanto essa blindagem altera o campo gravitacional.

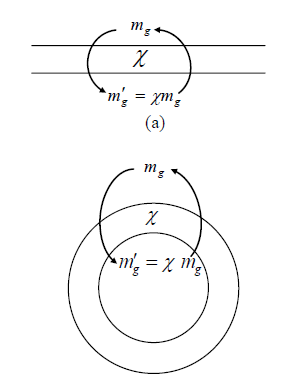
De forma mais completa, como ilustrado na figura, temos:

• Gravidade efetiva do lado A: $g_r + \chi \cdot g_r'$

• Gravidade efetiva do lado B: $g_r' + \chi \cdot g_r$

Esse comportamento evidencia que a blindagem modifica o campo gravitacional de forma ativa e direcionada, podendo tanto reduzir quanto anular ou até inverter parcialmente a força gravitacional sentida em determinada região.

Alcance do Efeito de Blindagem

A distância até onde esse efeito de blindagem gravitacional se propaga no espaço depende, essencialmente, da área superficial da blindagem:

• Quando usamos uma blindagem com superfície muito grande (por exemplo, um disco com raio $a$), experimentos mostram que o efeito pode se estender por uma distância aproximada de:

$$d \approx 20 \cdot a$$

Ou seja, se a blindagem tem 1 metro de raio, o campo modificado pode se propagar até 20 metros além da blindagem.

• Por outro lado, se a superfície da blindagem for muito pequena, o efeito se torna quase impossível de detectar experimentalmente, pois se restringe a uma região mínima.

Relação entre Massa Gravitacional e Massa Inercial pela Quantização da Gravidade

A quantização da gravidade sugere que a massa gravitacional $m_g$ e a massa inercial $m_i$ de uma partícula estão relacionadas por um fator dinâmico $\chi$, dado por:

$$\chi = \left\{ 1 - \left[ \frac{1}{120} \left( \frac{\Delta p}{m_i c} + 1 \right)^2 - 1\right] \right\}$$

onde:

• $m_i$ é a massa inercial de repouso da partícula;

• $\Delta p$ é a variação do momento linear da partícula;

• $c$ é a velocidade da luz no vácuo.

Essa fórmula mostra que a massa gravitacional de uma partícula pode variar de acordo com sua interação com campos de força (mecânicos, eletromagnéticos, etc.), desde que alterem seu momento linear.

Caso Particular: Absorção ou Emissão de Energia Eletromagnética

Se a variação do momento linear for resultado da absorção ou emissão de energia eletromagnética, então podemos escrever:

$$\Delta p = \frac{\Delta E}{c}$$

Substituindo isso na equação de $\chi$, obtemos:

$$\chi = \left\{ 1 - \left[ \frac{1}{120} \left( \frac{\Delta E}{m_i c^2} + 1 \right)^2 \right] \right\}$$

Além disso, ao dividir $\Delta E$ pelo volume da partícula $V$, considerando $\Delta E = \rho W V$, onde:

• $\rho$ é a densidade da matéria da partícula (em kg/m³);

• $W$ é a energia absorvida/emergida por unidade de massa (J/kg),

chegamos a uma expressão para $\chi$ em função da densidade:

$$\chi = \left\{ 1 - \left[ \frac{1}{120} \left( \frac{\rho W}{m_i c^2} + 1 \right)^2 \right] \right\}$$

Campo Gravitacional Repulsivo

Baseando-se nessa possibilidade, foi desenvolvido um método para gerar um campo de força gravitacional repulsivo, capaz de repelir fortemente partículas materiais. A ideia é utilizar um conjunto de blindagens gravitacionais esféricas, conforme mostrado na figura abaixo (vamos gerar uma imagem representativa em breve).

Considere um conjunto de blindagens esféricas com fatores $\chi_1, \chi_2, \dots, \chi_n$. Quando o sistema está desativado, a gravidade gerada pode ser aproximada por:

$$g_s \approx \frac{G m_i}{r^2}$$

onde $m_i$ é a massa inercial total do sistema.

Por outro lado, quando o sistema está ativado, cada blindagem modifica a massa gravitacional, resultando em:

$$m_g = m_i \cdot \chi_1 \chi_2 \dots \chi_n$$

E assim, a nova gravidade gerada será:

$$g_s' = \frac{G m_i \cdot \chi_1 \chi_2 \dots \chi_n}{r^2}$$

Se o produto dos $\chi_i$ for negativo ou suficientemente pequeno, o campo gravitacional resultante pode se tornar repulsivo.

Repulsão Gravitacional e Expulsão da Matéria

A equação estabelece que a pressão gerada por uma gravidade repulsiva $g'$, devido a uma massa gravitacional negativa, sobre a matéria ao redor da esfera pode ser expressa por:

$$p = \rho_{matter} \cdot g' \cdot \Delta S$$

Substituindo a expressão de $g'$ (gravidade modificada) da equação, temos:

$$p = \rho_{matter} \cdot \frac{G m_0}{r^2} \cdot \chi_1 \chi_2 \dots \chi_n \cdot \Delta S$$

Ou seja:

$$p = \Delta S \cdot \rho_{matter} \cdot \frac{G m_0}{r^2} \cdot \chi_{total}$$

Essa expressão indica que, se o produto dos fatores de blindagem gravitacional $\chi_i$ for negativo (com $n$ ímpar), o campo gravitacional torna-se repulsivo e exerce uma força de expulsão sobre a matéria ao redor. Isso gera uma pressão positiva direcionada para fora da esfera.

Condição para Expulsão da Atmosfera

Sabemos que a pressão atmosférica padrão ao nível do mar é aproximadamente:

$$p_{atm} \approx 1.013 \times 10^5 \, \text{Pa}$$

Para que toda a matéria — especialmente o ar — seja expulsa da região ao redor da esfera, é necessário que a pressão repulsiva supere esse valor:

$$p > p_{atm}$$

Substituindo isso na equação (9), obtemos a condição mínima para a blindagem gravitacional:

$$\rho_{air} \cdot \frac{G m_0}{r^2} \cdot \chi_1 \chi_2 \dots \chi_n > 1.013 \times 10^5 \, \text{Pa}$$

Se essa condição for satisfeita, todo o ar atmosférico será expulso da região em torno da esfera blindada gravitacionalmente — permanecendo apenas o Fluido Universal Contínuo (CUF), cuja densidade é extremamente pequena:

$$\rho_{CUF} \approx 10^{-27} \, \text{kg/m}^3$$

Interpretação Física

Esse mecanismo propõe, teoricamente, a possibilidade de criar uma zona de vácuo quase perfeito, não pela evacuação mecânica do ar, mas por um processo de repulsão gravitacional artificialmente induzida. Tal condição poderia ter implicações em propulsão sem reação, isolamento de campos, experimentação em condições extremas e muito mais.

Densidade do Fluido Quântico Universal (UQF)

Introduzindo um conceito fundamental:

A densidade do Fluido Quântico Universal (UQF) não é uniforme ao longo do Universo.

• Estado Supercomprimido → dá origem à matéria conhecida: quarks, elétrons, prótons, nêutrons, etc.

• Estado Normal (vácuo) → o fluido existe, mas não gera massa gravitacional. Ou seja:

  $$\chi = 0$$

Esse estado "normal" do fluido implica que não há efeito gravitacional, mesmo existindo inércia local. Mas, se houver matéria nas proximidades, ocorre um efeito de proximidade, e $\chi$ se torna ligeiramente diferente de zero, ou seja:

$$\chi \approx 0^{+}$$

Então, mesmo sem matéria diretamente presente, o UQF responde à vizinhança, gerando um valor quase nulo, mas diferente de zero, para a massa gravitacional.

Relações de Energia e Momento com Massa Gravitacional

A equação fundamental para a energia gravitacional relativística de uma partícula com massa gravitacional $m_g$ e velocidade $v$ é:

$$E_g = M_g c^2 \quad \text{(Eq. 11)}$$

onde:

$$M_g = \frac{m_g}{\sqrt{1 - \frac{v^2}{c^2}}} \quad \text{(Eq. 12)}$$

E como $m_g = \chi m_i$, temos:

$$M_g = \frac{\chi m_i}{\sqrt{1 - \frac{v^2}{c^2}}}$$

Logo:

$$E_g = \chi m_i c^2 \left( \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} \right) \quad \text{(Eq. 13)}$$

Momento Quântico e Relação de De Broglie Generalizada

A equação para o momento quântico gravitacional com fator $\chi$ é:

$$q = M_g v = \chi m_i \frac{v}{\sqrt{1 - \frac{v^2}{c^2}}}$$

e a relação de comprimento de onda generalizada é:

$$\lambda = \frac{h}{q} = \frac{h}{\chi m_i \cdot \frac{v}{\sqrt{1 - \frac{v^2}{c^2}}}} \quad \text{(Eq. 14)}$$

Agora, no limite relativístico $v \rightarrow c$:

• Se $m_i \neq 0$, o momento e a energia tendem ao infinito, ou seja: partículas com massa não podem atingir a velocidade da luz.

• Para partículas sem massa inercial ($m_i = 0$), como os fótons, a equação fornece:

$$\lambda = \frac{h}{q} = \frac{h}{\chi m_i v} \Rightarrow \lambda = \frac{h}{q}, \text{ para } \chi = 1$$

Logo, a relação de De Broglie clássica:

$$\lambda = \frac{h}{p}$$

é apenas um caso particular do modelo mais geral, quando $\chi = 1$.

Conclusão e Interpretação

Esse modelo oferece uma interpretação estendida da gravidade quântica e sua relação com a matéria, energia, e a constante $\chi$:

• A massa gravitacional não é uma propriedade absoluta, mas relacional, dependendo do estado do UQF e de sua vizinhança.

• A constante $\chi$ mede o acoplamento entre massa inercial e massa gravitacional, e varia conforme as interações do UQF.

• A teoria oferece um mecanismo para a gravidade repulsiva e expulsão da matéria, e generaliza as relações relativísticas e quânticas fundamentais.

Quantização da Gravidade

• Relação entre massa gravitacional e inercial:

  $$m_g = \chi \cdot m_i$$

  Onde:

  • $\chi$ depende da variação do momento $\Delta p$

  • $\Delta p = F \cdot \Delta t$ (não importa a natureza da força)

• Se energia eletromagnética é absorvida:

  $$\chi = \left\{1 - \left[\left(\frac{\Delta E}{m_i c^2} + 1\right)^2\right]^{-1}\right\}$$

Blindagem Gravitacional (GS)

• A blindagem reduz a gravidade de um lado da estrutura:

  $$g' = \chi \cdot g$$

• Com múltiplas blindagens esféricas:

  $$g_s = \frac{G m_s}{r^2} \quad \text{e} \quad m_g = \chi_1 \chi_2 \cdots \chi_n \cdot m_s$$

Expulsão de Matéria

• Quando $\chi_n < 0$ (n ímpar), cria-se uma repulsão gravitacional:

  $$p = \Delta g \cdot \rho_{\text{matéria}} \cdot S$$

• Se:

  $$\Delta p > 10^5 \, \text{Pa}$$

  ➜ Toda a matéria (exceto o Fluido Universal) é expulsa da região

4. Fluido Quântico Universal (CUF)

• Densidade:

  $$\rho_{\text{CUF}} \approx 10^{-27} \, \text{kg/m}^3$$

• No estado normal:

  $$\chi = 0 \Rightarrow m_g = 0$$

• Com proximidade de matéria:

  $$\chi \rightarrow 0^+ \Rightarrow m_g \approx 0^+$$

Energia e Momento Gravitacional

• Energia:

  $$E_g = M_g c^2 \quad \text{com} \quad M_g = \frac{m_g}{\sqrt{1 - v^2/c^2}}$$

• Momento quântico:

  $$q = \chi \cdot \frac{h}{\lambda}$$

• Para $\chi = 1$, recupera-se a equação de De Broglie:

  $$q = \frac{h}{\lambda}$$

Redução de χ ⇒ Redução de Energia Gravitacional e Momento

• De acordo com:

  $$E_g = \chi \cdot M_i c^2 \quad \text{e} \quad q = \chi \cdot \frac{h}{\lambda}$$

• Se $\chi \to 0$, então:

  • $E_g \to 0$

  • $q \to 0$

  • Implicação: partículas e fótons, inclusive infravermelhos, têm energia e momento praticamente nulos.

Isolamento Térmico Perfeito

• Com $E_g \approx 0$ dos fótons:

  • A radiação térmica não interage com a nave.

  • A nave pode penetrar o Sol e sair sem dano.

  • Tripulação protegida da temperatura extrema.

Redução de Atrito Atmosférico

• O campo gravitacional repulsivo reduz o atrito com o ar:

  • Viagens em alta velocidade sem superaquecimento.

  • Ideal para aeronaves hipersônicas ou de reentrada.

Baixa Massa Gravitacional da Nave

• Considerando blindagens esféricas com:

  $$m_g = \chi_1 \chi_2 \cdots \chi_n \cdot m_s$$

  • Com 7 camadas:

    $$\chi^n \approx 0.071 \Rightarrow m_g \ll m_i$$

  • Peso da nave se torna muito pequeno.

  • Mesmo pequenos empuxos causam grandes acelerações:

    $$a = \frac{F}{m_g}$$

Construção das Blindagens

• Material com:

  • Densidade $\rho$

  • Índice de refração $n_r$

  • Aplicação de campo elétrico:

    $$E = W / (\epsilon)$$

• Permite ajuste fino de $\chi$, conforme equação (5).

Supernave Gravitacional

• Nave com:

  • Massa gravitacional quase nula

  • Inércia quase imperturbada por forças externas

  • Isolamento térmico perfeito

  • Baixíssimo atrito atmosférico

Neste trabalho, exploramos a teoria da quantização da gravidade, focando na relação entre a massa gravitacional $m_g$ e a massa inercial $m_i$, conectadas por um fator de correlação $\chi$. Demonstrou-se que esse fator pode ser modificado conforme a variação do momento cinético da partícula, $\Delta p$, que por sua vez depende da força aplicada ao longo de um intervalo de tempo $\Delta t$. Essa variação pode estar relacionada, por exemplo, à absorção ou emissão de energia eletromagnética.

Através da densidade de energia por volume, obtivemos uma equação fundamental:

$$\chi = 1 - \left( \frac{\Delta W}{\rho c^2} \right)$$

Essa expressão nos permitiu concluir que, sob certas condições, é possível reduzir drasticamente o valor de $\chi$, o que leva à redução da massa gravitacional de uma partícula ou de um sistema.

Com isso, apresentamos o conceito de campo de força gravitacional repulsivo, baseado em um conjunto de esferas de blindagem gravitacional, cujos fatores $\chi_1, \chi_2, ..., \chi_n$ são ajustados para valores negativos (com $n$ ímpar). O efeito resultante é uma força de repulsão que atua sobre a matéria externa, gerando pressão gravitacional negativa capaz de expulsar a matéria da região ao redor das esferas — como, por exemplo, o ar atmosférico.

A região então se torna ocupada exclusivamente pelo Fluido Quântico Universal (CUF), cuja densidade é extremamente baixa, mas cuja massa gravitacional torna-se diferente de zero devido ao efeito de proximidade com matéria externa.

A teoria mostra ainda que o momento gravitacional e a energia gravitacional de partículas e fótons podem ser praticamente anulados em regiões onde $\chi \rightarrow 0$. Isso abre possibilidade para propriedades extraordinárias como:

• Isolamento térmico absoluto, tornando possível, teoricamente, que uma espaçonave atravesse até mesmo o Sol sem ser afetada.

• Redução do atrito atmosférico, possibilitando velocidades elevadíssimas sem superaquecimento.

• Aceleração extrema com pequeno impulso, devido à redução da massa gravitacional da nave.

• Gravidade quase nula, facilitando o deslocamento no espaço e em atmosferas planetárias.

Ao final, fornecemos um valor de referência para $\chi^n \approx 7.00 \times 10^{-22}$, mostrando que é teoricamente viável construir esse sistema com materiais de densidade conhecida e índice de refração apropriado, utilizando campos eletromagnéticos intensos.

Conclusão

A teoria aqui desenvolvida propõe uma profunda revisão do entendimento tradicional da gravidade, ao introduzir o fator de correlação $\chi$ como elemento chave para a distinção entre massa inercial e gravitacional. Através da manipulação desse fator com campos eletromagnéticos, a teoria oferece fundamentos para a criação de campos gravitacionais repulsivos e escudos gravitacionais capazes de isolar completamente regiões do espaço de interferências térmicas e gravitacionais externas.

A aplicação prática dessa teoria pode revolucionar o campo da propulsão espacial, permitindo a construção de naves com capacidade de atravessar meios extremos como a atmosfera terrestre em alta velocidade ou mesmo o interior do Sol, sem danos estruturais ou riscos à tripulação. Além disso, os efeitos de anulação de energia e momento gravitacional apontam para possibilidades inexploradas no controle da inércia e da termodinâmica.

Embora a proposta exija validações experimentais rigorosas, os fundamentos matemáticos e conceituais apresentados indicam um novo caminho para o entendimento das interações gravitacionais em nível quântico e para o futuro da engenharia aeroespacial.

Referências Bibliográficas

1. Einstein, A. (1915). Die Feldgleichungen der Gravitation. Königlich Preußische Akademie der Wissenschaften (Berlin), Sitzungsberichte.

2. De Broglie, L. (1924). Recherches sur la théorie des quanta. PhD Thesis, Paris.

3. Feynman, R. P., Leighton, R. B., & Sands, M. (1964). The Feynman Lectures on Physics. Addison-Wesley.

4. Misner, C. W., Thorne, K. S., & Wheeler, J. A. (1973). Gravitation. W. H. Freeman and Company.

5. Weinberg, S. (1972). Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity. John Wiley & Sons.

6. Dirac, P. A. M. (1930). The Principles of Quantum Mechanics. Oxford University Press.

7. Higgs, P. W. (1964). Broken Symmetries and the Masses of Gauge Bosons. Physical Review Letters, 13(16), 508–509.

8. Fontinele, M. (2025). Notas sobre a interação gravitacional quantizada e aplicação de campos repulsivos. Estudo independente.